Survival of the Fittest

The survival analysis methodology, applied to both individuals and social structures, shows that marriages and states do not "age" in the traditional sense. After overcoming initial risks, their likelihood of "death" remains almost unchanged over time, making these structures, unlike individuals, practically immortal.

In one of the previous posts, we discussed how Roman emperors can be analyzed using survival analysis methodology. Today, we will explore other aspects of human life where this methodology can be applied.

Survivorship Curves in Wild Nature

Survivorship curves illustrate what proportion of organisms survive to a certain age. Generally, three types of these curves are distinguished:

• Type I is characterized by high survivorship in the early and middle parts of life, followed by a rapid decline in late life. These curves are typical for species with small offspring numbers and significant parental care (known as K-selected species), including humans and most mammals, such as elephants.
• Type II, resembling a straight line, corresponds to a roughly constant probability of death throughout life. This type includes some birds and lizards.
• Type III is characterized by high mortality in early life and comparatively high survivorship for those who reach middle age (r-selected species). This category includes most marine animals and, for example, trees.

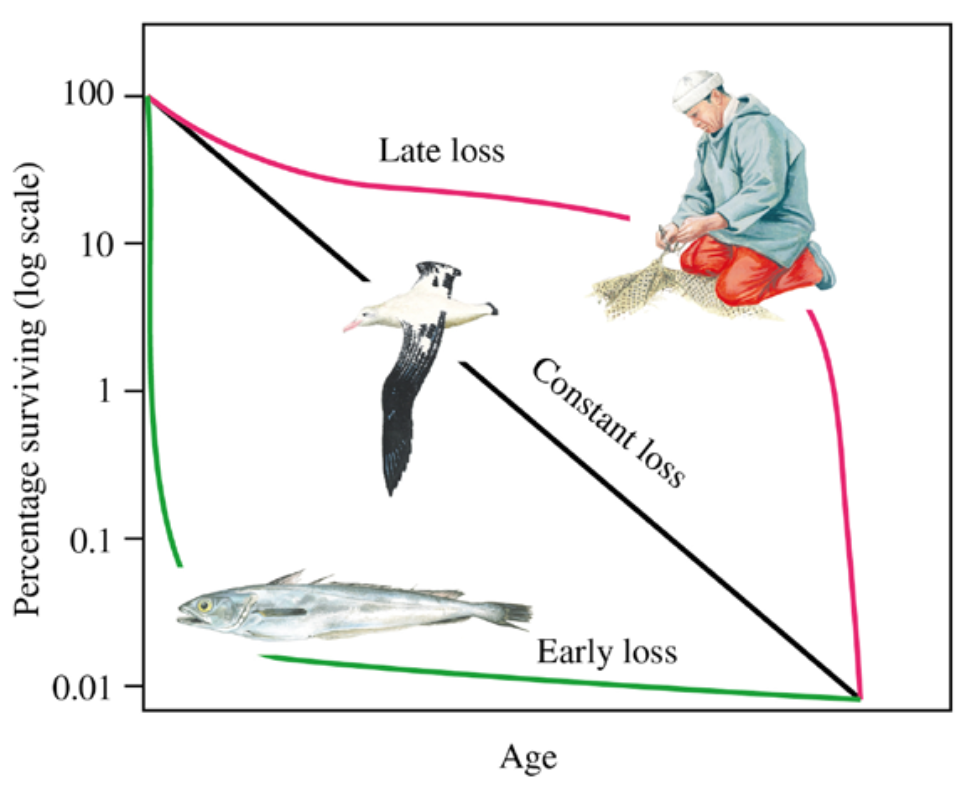
Of course, the division into types is quite conditional, and in reality, the curves can exhibit more complex patterns, as we observed when discussing Roman emperors. An analogous concept to survival analysis in biology is life history theory, which examines various life strategies and the reasons for their selection.

Humans

Historically, humans have been characterized by relatively high infant mortality (though not nearly as high as that of r-species), a consistently low mortality rate in middle age, and then a steadily increasing mortality rate as life expectancy nears its end. Gradual improvements in living conditions have led to a noticeable change in the survivorship curve—it is trending toward a more rectangular shape. Notably, the maximum lifespan has remained virtually unchanged.

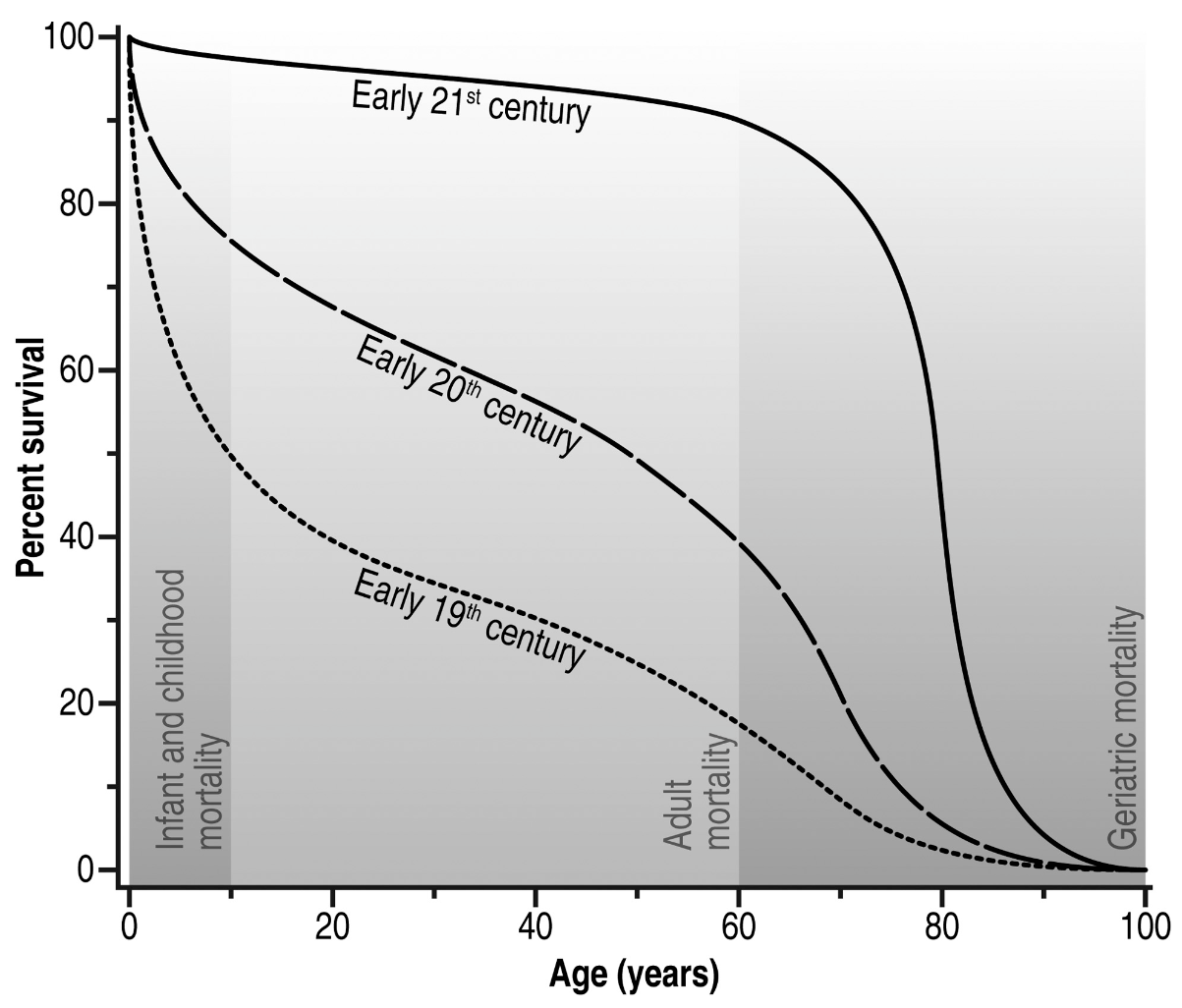
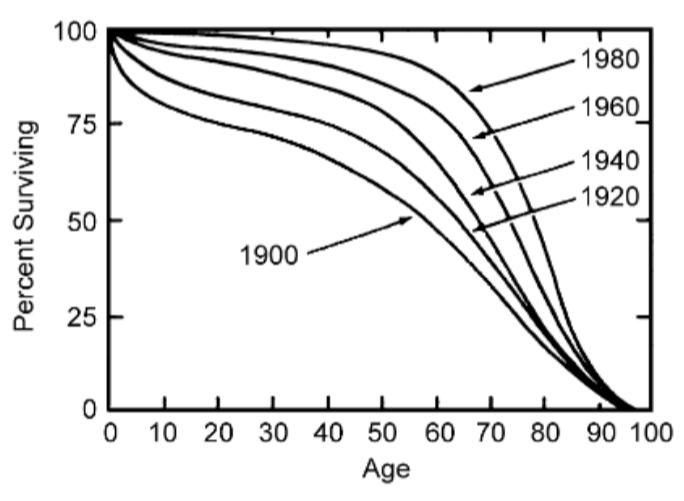
Marriages

Now that we have clarified the nature of the curves for individuals, it becomes interesting to consider the characteristics of the social structures that people create. Let’s start with one of the simplest—marriage.

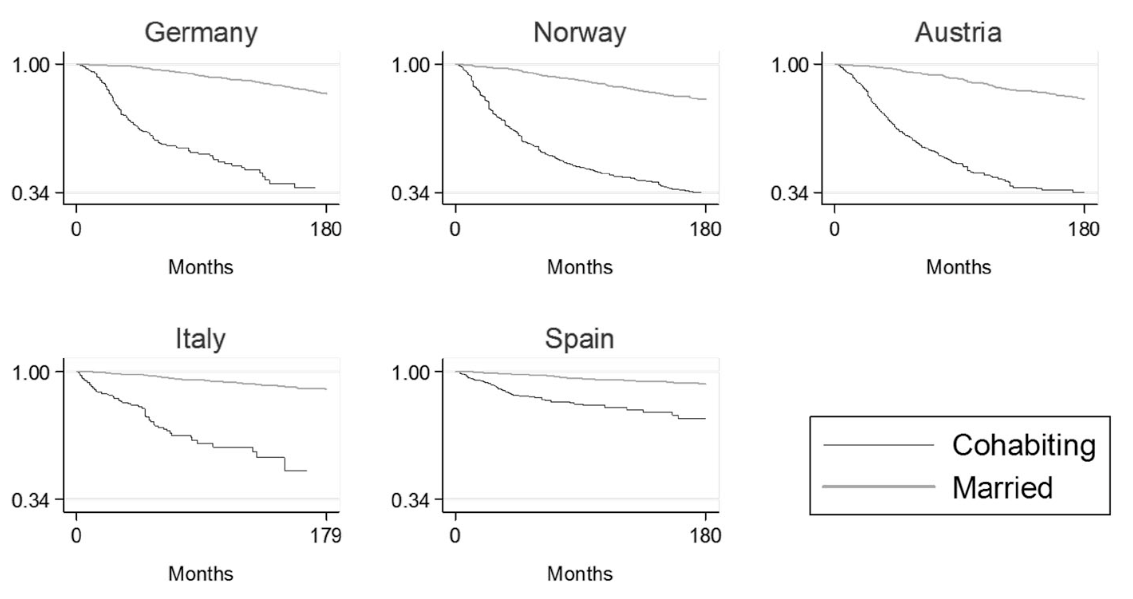
The graphs below present the survivorship curves for marriages and cohabitations (in this case, the difference between them is not significant for us) in five European countries at the beginning of the 21st century [4].

The next graph discusses marriages in a relatively traditional society, such as the Amdo Tibetans in China (again, the nuances of how dowries influence marriage survivorship are not our concern at this point) [5].

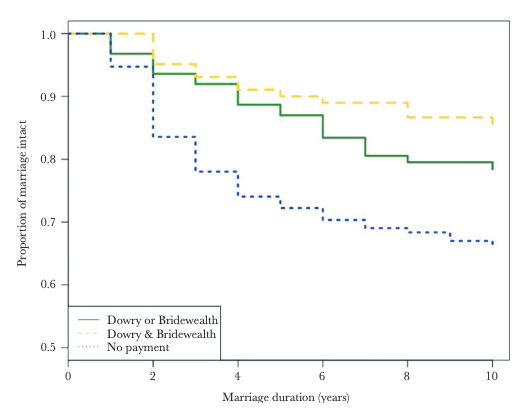
In both cases curves are characterized by the absence of a downward bend at long marriage durations. In other words, marriages can be classified as belonging to Type II or III survivorship curves. There exists a certain number of "failed" marriages that dissolve shortly after being formed, followed by a nearly constant "mortality" rate influenced by random factors. Importantly, marriage does not "age."

States

On the other end of the spectrum of social structures are states. A recent article explores the topic of their survivability in depth[6]. The analysis used two databases: the internally created MOROS (MORtality Of States) and the publicly available Seshat, which you can find a link to in our library. Below is a histogram showing the duration of states founded before 1800.

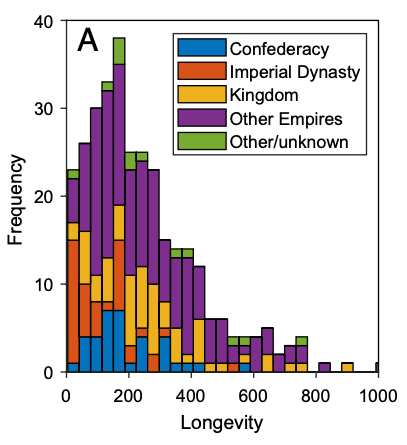
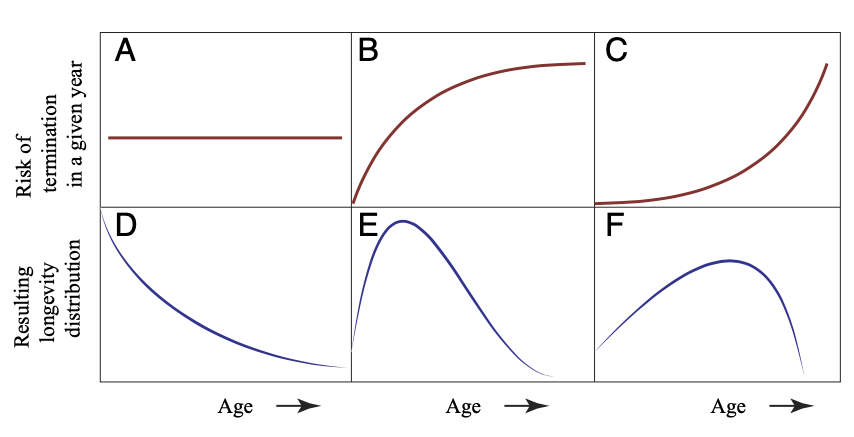
Based on this histogram, we can infer the risks that threaten states. If the risk were time-independent (subfigure A below), the distribution of states by lifespan would take on an exponential shape (D, Type II survivorship curves, akin to what we observe in birds). If the risk increases over time (C), the distribution would exhibit a pronounced sharp decline with age (F, Type I in animals, similar to humans under modern conditions). Finally, if the risk ceases to grow over time (B), we would obtain a distribution resembling a log-normal curve (E), consistent with the data extracted from the databases.

Indeed, if we approximate the obtained distributions by lifespan, we can calculate both the hazard function (risk of death) and the survivorship curve. We observe that the risks of state collapse increase until an age of about 200-300 years and then become constant. Results are slightly different for two databases, but general conclusion is true in both cases.

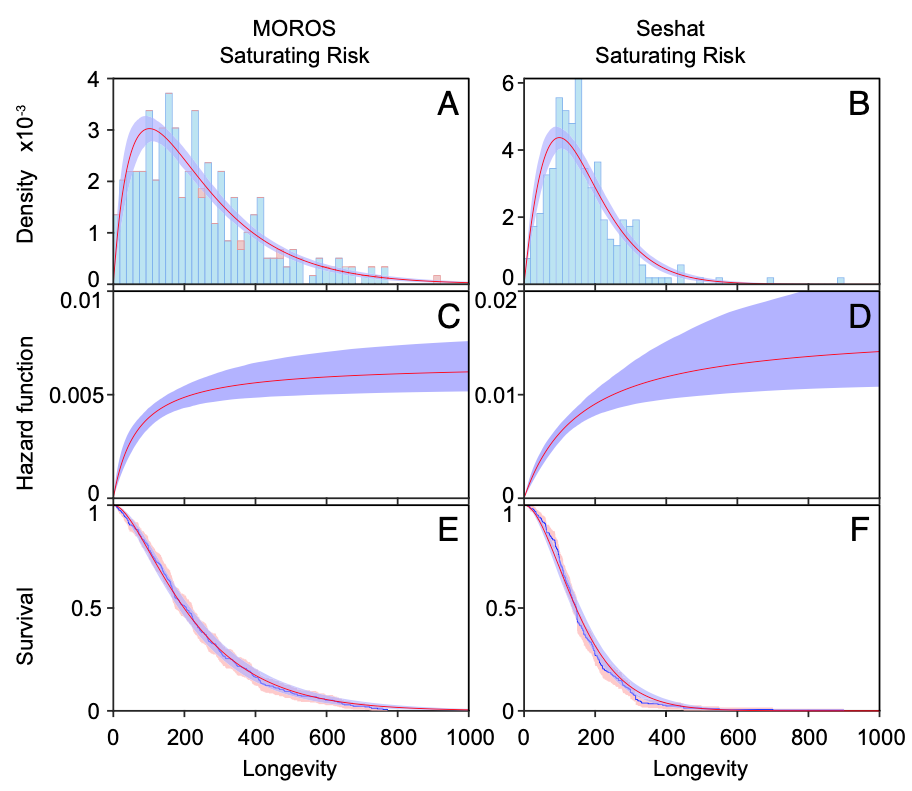
This means that creating a state is probably such a significant task, requiring substantial resources, that a newly established state has a certain buffer of resilience. There is no increased "infant" mortality for states. Over time, risks grow, and the state system is subjected to new challenges of various kinds, but if it demonstrates sufficient resilience, it reaches "adulthood." From that point on, its demise becomes a random factor. Contrary to common beliefs, there is no evidence of state "aging," or increased risk of death with age.

Conclusion

Humans have a finite lifespan. Progress in medicine and living conditions over the past centuries has altered the shape of the survivorship curve, but has little changed the maximum lifespan. In contrast to individuals, the social structures they create appear to be immortal in the sense of lacking a maximum lifespan (this may sound counterintuitive regarding marriage, but we do not consider the end of marriage due to the death of one spouse as its "own" death). We observe that for both marriages and states, the risks of death are close to being independent of age (at least after reaching a certain point).

Sources:

[1] Caddy, J. F. (2015). Criteria for sustainable fisheries on juveniles illustrated for Mediterranean hake: control the juvenile harvest, and safeguard spawning refugia to rebuild population fecundity. Scientia Marina, 79(3), 287-299.
[2] Fries, J. F. (1984). The compression of morbidity. In Aging and Technological Advances (pp. 169-187). Boston, MA: Springer US.
[3]Mulligan, V. K., & Chakrabartty, A. (2013). Protein misfolding in the late‐onset neurodegenerative diseases: Common themes and the unique case of amyotrophic lateral sclerosis. Proteins: Structure, Function, and Bioinformatics, 81(8), 1285-1303.
[4] Rutigliano, R., & Esping-Andersen, G. (2018). Partnership choice and childbearing in Norway and Spain. European Journal of Population, 34, 367-386.
[5] Du, J., & Mace, R. (2019). Marriage stability in a pastoralist society. Behavioral Ecology, 30(6), 1567-1574.
[6] Scheffer, M., Van Nes, E. H., Kemp, L., Kohler, T. A., Lenton, T. M., & Xu, C. (2023). The vulnerability of aging states: A survival analysis across premodern societies. Proceedings of the National Academy of Sciences, 120(48), e2218834120.