Roma Caput Mundi

If you could show the cabbage I planted with my own hands to your emperor, he definitely wouldn’t dare suggest I replace the peace and happiness of this place with the storms of a never-satisfied greed.

Diocletian, the first Roman emperor to abdicate the position voluntarily

When we talk about psychohistory, we often emphasize the need for studying large groups of people. This usually means analyzing groups that exist at a particular moment in time. A recent article [1] approaches this challenge from a different angle – it explores groups of individuals who share common traits but are separated in time by decades or even centuries. The focus of the article is on Roman emperors, specifically examining the circumstances of their deaths.

Data

From the time of Augustus, who first assumed the title of emperor in 27 BC, until Theodosius, whose death in 395 AD marked the final division of the Empire into Western and Eastern halves, the Roman throne was occupied by 69 rulers. Out of these, 43 met a violent end. Thus, the likelihood of a newly ascended emperor being killed in some manner was around 62%. For comparison, the risk for climbers conquering 8,000-meter peaks in the Himalayas is just 4%, and for players of Russian roulette, it’s under 17%. To match the risks of a Roman emperor’s life with Russian roulette, you would need to load 4 bullets into a six-chamber revolver.

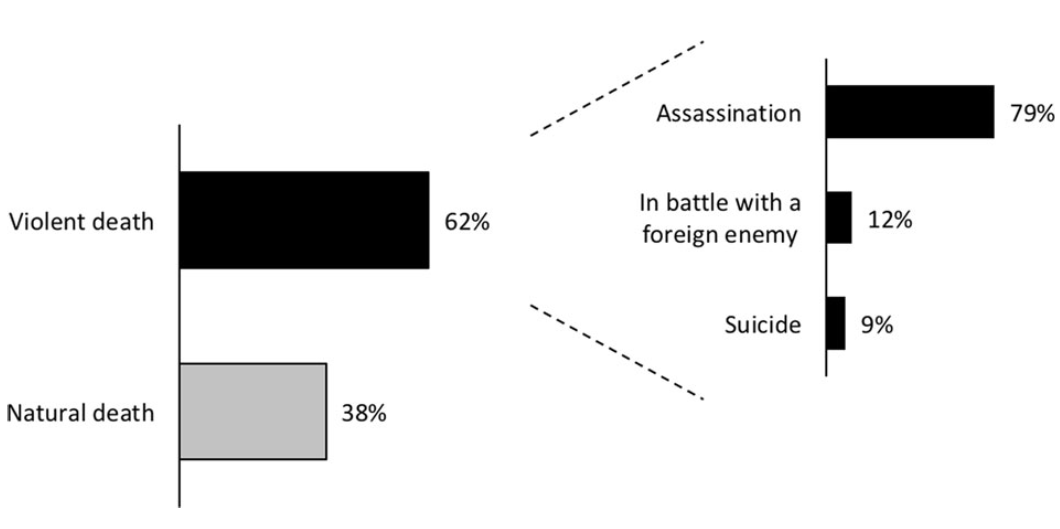
The immediate causes of death for most emperors are well-documented in historical literature, but can we generalize them in any way? It turns out that we can, using concepts from reliability engineering. This field is based on two main concepts: time-to-failure, a random variable representing the moment when a mechanism or part fails, and reliability, which is the probability that a mechanism or part continues to function up to a given time.

The chart below illustrates the relationship between reliability over time, or, in other words, the survival function for emperors who met a violent end. As shown, from the 100% of emperors who ascended to the throne at time zero, approximately 70% would survive to their second anniversary, just under half would make it to their tenth year, and only 30% would have a reign lasting longer than 16 years. In other words, 70% of emperors would be killed before reaching a 16-year reign.

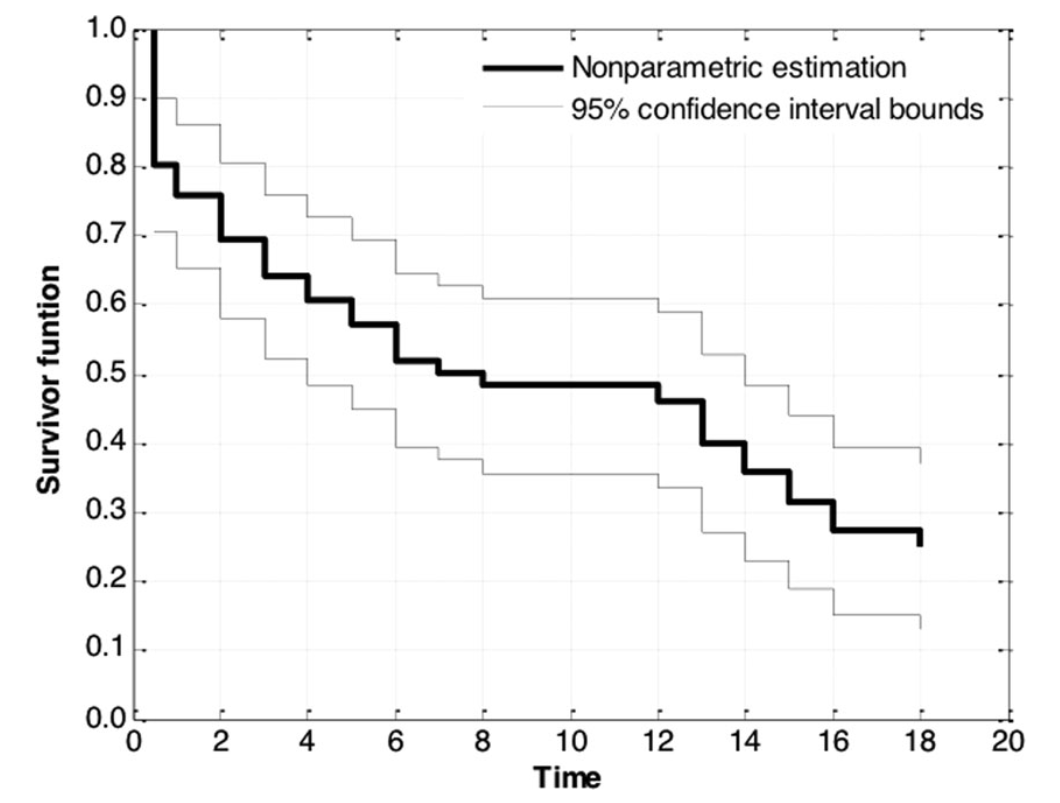
The author describes the graph as follows:

i. Emperors faced a notably high risk of violent death during their first year in power. This risk remained elevated but gradually decreased over the next seven years. This pattern is similar to the "infant mortality" phase in reliability engineering, where weak components fail early due to design or manufacturing defects. Thus, Roman emperors experienced a form of infant mortality.

ii. The reliability or survival function stabilizes around the eighth year of rule. If emperors managed to reach this milestone, they could somewhat lower their guard...

iii. ...but not for long: the risk of violent death surged again after twelve years of rule. This suggests that new mechanisms or processes initiated another wave of violence. This phenomenon resembles the "wear-out period" in reliability engineering, where the failure rate of components increases due to fatigue, corrosion, or wear. Consequently, Roman emperors also experienced wear-out mortality.

Interpretation

If the deaths of emperors occurred completely at random, the survivor function would resemble a simple exponential function with no inflection points. Since the actual function shows a different pattern, it implies that the causes of death follow a certain pattern.

The author draws inspiration from reliability engineering and examines two classic problems from this field. First, if a system consists of n components and the failure of any one of them leads to the breakdown of the entire system, the time-to-failure of the system can be described by a Weibull distribution (with a sufficiently large n, it becomes irrelevant how the individual components' time-to-failure is distributed). Second, if the system is monolithic, meaning it cannot be divided into components, but is subject to n different external factors trying to break it, the time-to-failure of the system also follows a Weibull distribution, regardless of the properties of the external factors.

What is this function? Mathematically, it is expressed simply as:

S(t) = exp(t/f)^b,

where S represents reliability, t is time, and f and b are parameters describing the specific distribution. If b < 1, it indicates a prevalence of infant mortality, meaning a decreasing failure rate over time. If b > 1, it indicates wear-out mortality, where the failure rate increases over time.

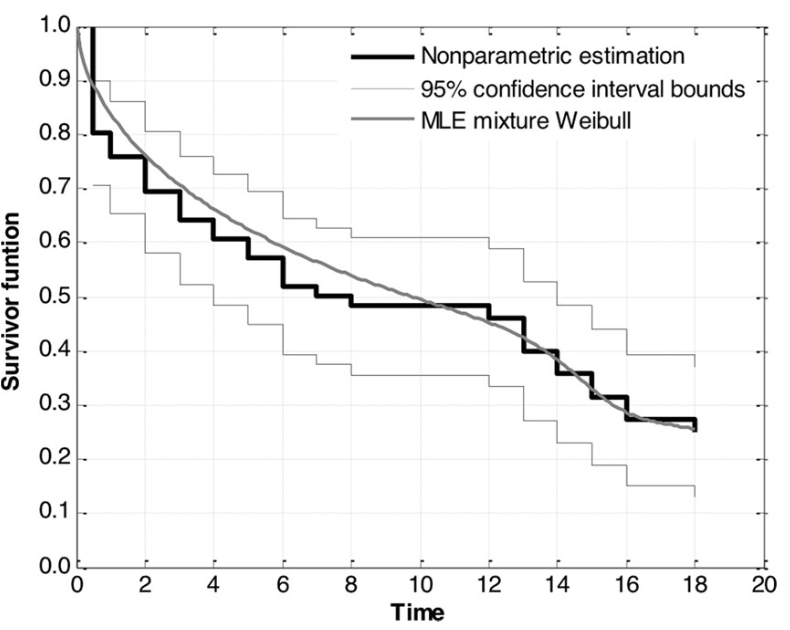
It turns out that the survivor function of Roman emperors is best fitted by a combination of two Weibull functions: one representing predominant infant mortality and the other representing wear-out mortality, as illustrated below.

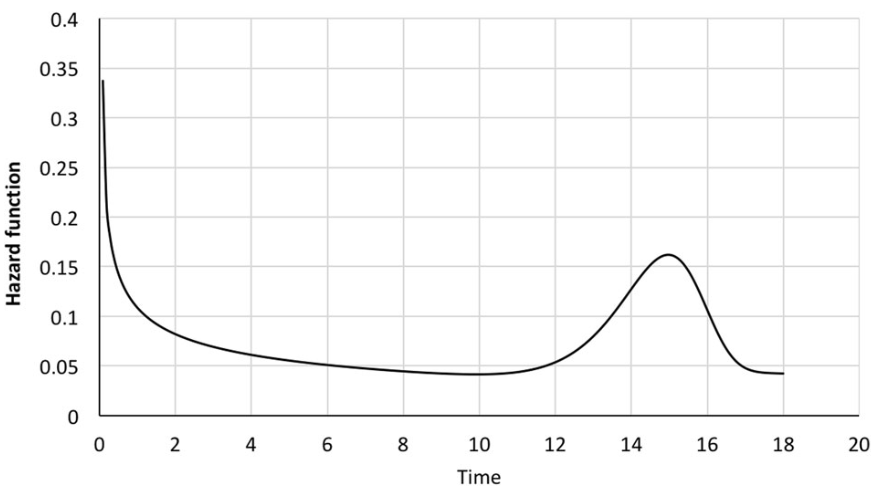
For the fitted model, we can construct the failure rate as a function of time, which represents the likelihood of an emperor being assassinated in any given year. This function takes on a characteristic U-shape, commonly observed in most mechanical systems and components. In the early years of rule, we see a high rate of infant mortality. Those who accidentally ascend to the throne, unfit for leadership, are quickly eliminated, much like faulty components that fail before their warranty period. After around 12 years of rule, there is a noticeable rise in wear-out mortality. Emperors, accustomed to a specific style of governance, encounter new external and internal challenges, and their flexibility diminishes with age and experience, eventually leading to their demise—much like parts that have outlived their usefulness.

After all, the emperor is just a cog in the Imperial machine.

Conclusion

As the author notes:

Roughly speaking, the result implies the existence of systemic factors and some level of determinism, in an average sense or expected value, superimposed on the underlying randomness of the phenomenon here examined. In other words, the process is not completely aleatory; it has some deterministic factors overlaid on its randomness.

Is this not a reflection of the laws of psychohistory at work?

Sources:

[1] Saleh, J.H. Statistical reliability analysis for a most dangerous occupation: Roman emperor. Palgrave Commun 5, 155 (2019).